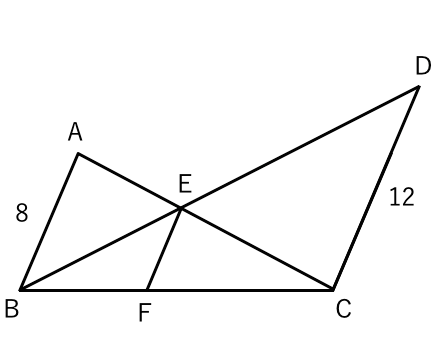
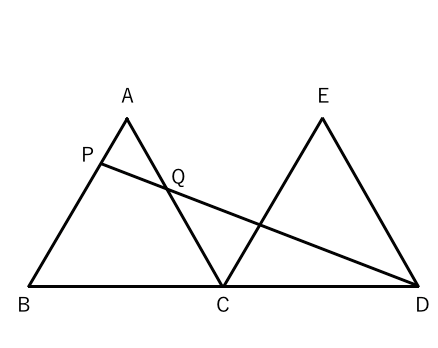
面白い数学図形問題 (中3) カテゴリ: カテゴリ未分類 中2の K衛門 。 やはりカンどころがよくて、もうすっかり図形の苦手意識がなくなっている。 期末テスト数学は予定通り (? )余裕で100点。 で、先生から数学のライバルの子と2人だけに 特別出された 基本的な問題は難しくないのでしっかり確認しておいてください。 よくある相似の証明 1 下の図で abcと decが相似であることを証明。 証明 abc∽ dec *∠bac=∠edcを利用して証明してもよい 2 下の図で aceと bdeが相似であることを証明。 ace∽ bde問題(後期期末) 右の図のように,アとイの相似比が1:k である2 つの相似な五角形をそれぞれ3 つの三角形に分け,各 三角形の面積をX,Y,Z および,X',Y',Z'とす る。このとき,対応する三角形はそれぞれ相似で,相 似比はすべて1:k である。
中3数学 相似や比の応用問題を解くためのテクニック 個別指導塾のyou 学舎日記 公式ブログ
数学 相似 問題 難問
数学 相似 問題 難問-相似な図形 テストに出やすい問題 ※図形クリックで拡大 (1)右の図で,点Pは線分ACとBDの交点であり,AB//DCである。 点Pを通り,ABに平行な直線を引き,BCとの交点をQとする。 AB=18cm,CD=12cm,BD=18cmとするとき,次の問いに答えなさい。 ①PQの長さを求めなさい。 ②PDの長さを求めなさい。 (2)右の図で,平行な直線a,b,cが直線dとそれぞれA,D,E中学数学 \(y=ax^2\) 図形との融合問題 中学数学 \(y=ax^2\) 放物線と直線の交点;




中3数学 相似 台形の対角線 Youtube
相似3 次の問いに答えよ。 図でa,b,c,dはすべて円周上の点である。ae=12cm,ce=9cm, de=4cmのときbeの長さを求めよ。 a b c d e 図で∠ 応用問題を解くには、当然、基本が分かっていないとできません。 ということで、まずは相似(合同)や比の問題で最初にやることを確認しておきます。 ①与えられた長さ、角度、比は図に書き込む ②比を求めたい場合は、比を求めたい直線を、1辺とし相似な立体の表面積・体積(2) 6 円 円周角と中心角(1) 問題一括 (2,462Kb) 解答一括 (2,734Kb) 円周角と中心角(2) 円周角と中心角(3) 等しい弧と円周角 円周角と図形の証明 円周角の定理の逆 円周角の定理の活用 7 三平方の定理 三平方の定理の証明(1) 問題一括 (3,793Kb) 解答一括
相似な図形 について 無料で使える中学学習プリント 中学生向けの数学、理科、社会、漢字などの問題プリントをpdfで配布しています。 コンテンツへスキップ ナビゲーションに移動問題集 ~ スタディエイドで作成した問題です。 リンクをクリックするとpdfが開きます。 中学1年生 問題 (ページ数) 解答 (ページ数) 1章 正の数・負の数 問題 (6p) 解答 (6p) 2章 文字の式証明問題 (合同・相似)の解き方 21年2月1日 学習内容解説ブログサービスリニューアル・受験情報サイト開設のお知らせ 学習内容解説ブログをご利用下さりありがとうございます。 開設以来、多くの皆様にご利用
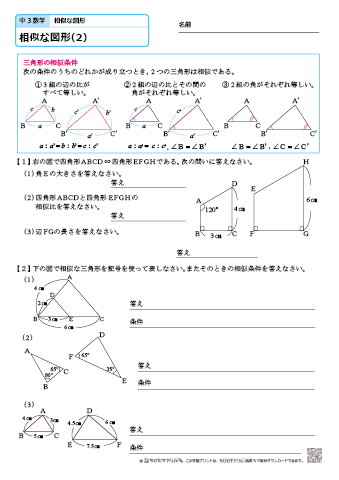
数学35章図形と相似「相似な図形」<準備問題①> 組 番 名前 1三角形の合同条件を書きなさい。 2次の図で,AB//CDのとき,次の問いに答えなさい。図形・相似 中学数学相似とは何か・導入 中学数学三角形の相似条件 中学数学相似の証明・その1 中学数学相似の証明・その25章 図形と相似 愛知県公立高校入試(数学) ~単元別過去問~ 問題プリントと解答・解説 ホーム 情報&分析 オンライン・ICT 公立対策 私立対策 国立高専 定時制 単元別




三角形の相似条件が見やすい図で一発理解できる 練習問題付き 高校生向け受験応援メディア 受験のミカタ



中学数学相似 この問題を教えて欲しいです Yahoo 知恵袋
ついに出ました! 正解率0%です。 平成25年度 岐阜県 数学 問4 (2)(イ) 正解率 0% 上の図で、4点 a、b、c、d は 円o の周上にあり、ac は 円o の直径で、ah は 三角形 abd中学数学の問題ソフト無料 中1数学 正負の数,文字と式,1次方程式,比例・反比例,平面図形,空間図形,資料の活用 中2数学 式の計算,連立方程式,1次関数,図形の性質,確率 中3数学 式の計算,平方根,2次方程式,2次関数,相似な図形,円周角,三平方の定理,標本相似の証明問題 中3数学で学ぶ「相似の証明問題」のテストによく出る問題(練習)を学習しよう! 図形の相似の問題を見る > すべての授業の「要点まとめノート」「問題・解答」をPDF無料ダウンロードできる 学校で使っている教科書にあわせて勉強できる わからないところを質問できる 会員登録をクリックまたはタップすると、 利用規約・プライバシー
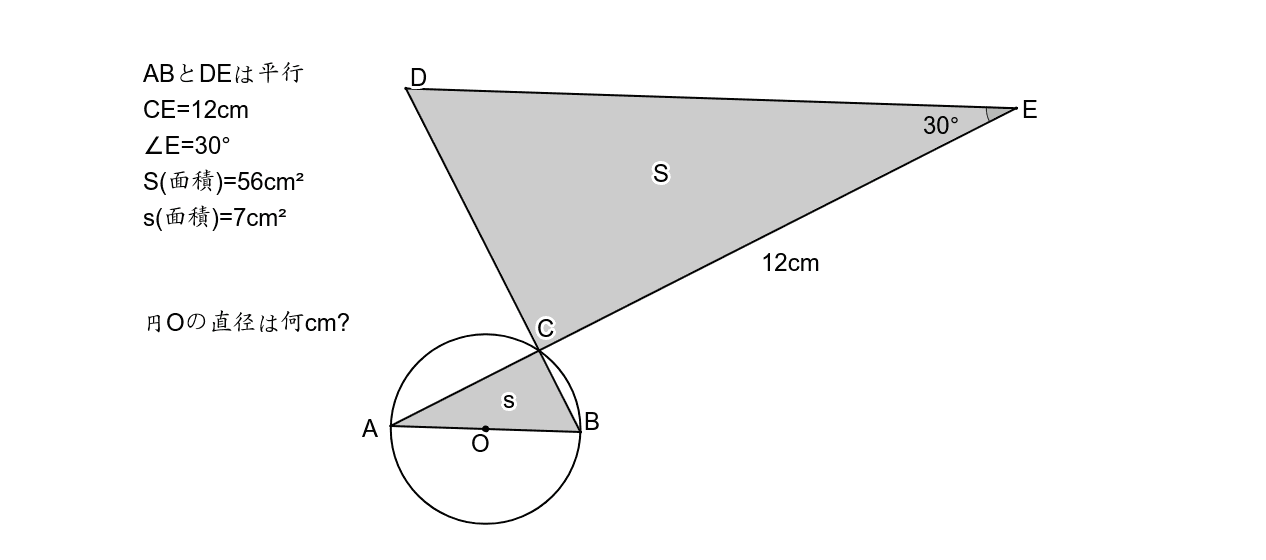



数学3 相似 円 複合問題 Geogebra



1
相似 相似1(基礎) 相似2 相似の証明1 相似の証明2 相似と線分比1 相似と線分比2 相似と線分比3 相似と線分比4(発展) 相似5 相似6 角の二等分線と辺の比(発展) 相似と面積比 面積比相似な図形と線分比と平行の関係、その計算方法と図形をとらえる視点について応用問題を含めて学習します。 三角形と線分比 平行線と線分比 線分比と相似 線分比と相似 線分比と相似 線分比と相似 線分比と相似 線分比と相似相似2 図でac//deである。 a b c d e abc∽ ebdを証明しなさい。 ac=15cm, de=10cm, be=6cmのときabの長さを求めよ。 図でde//bcである。
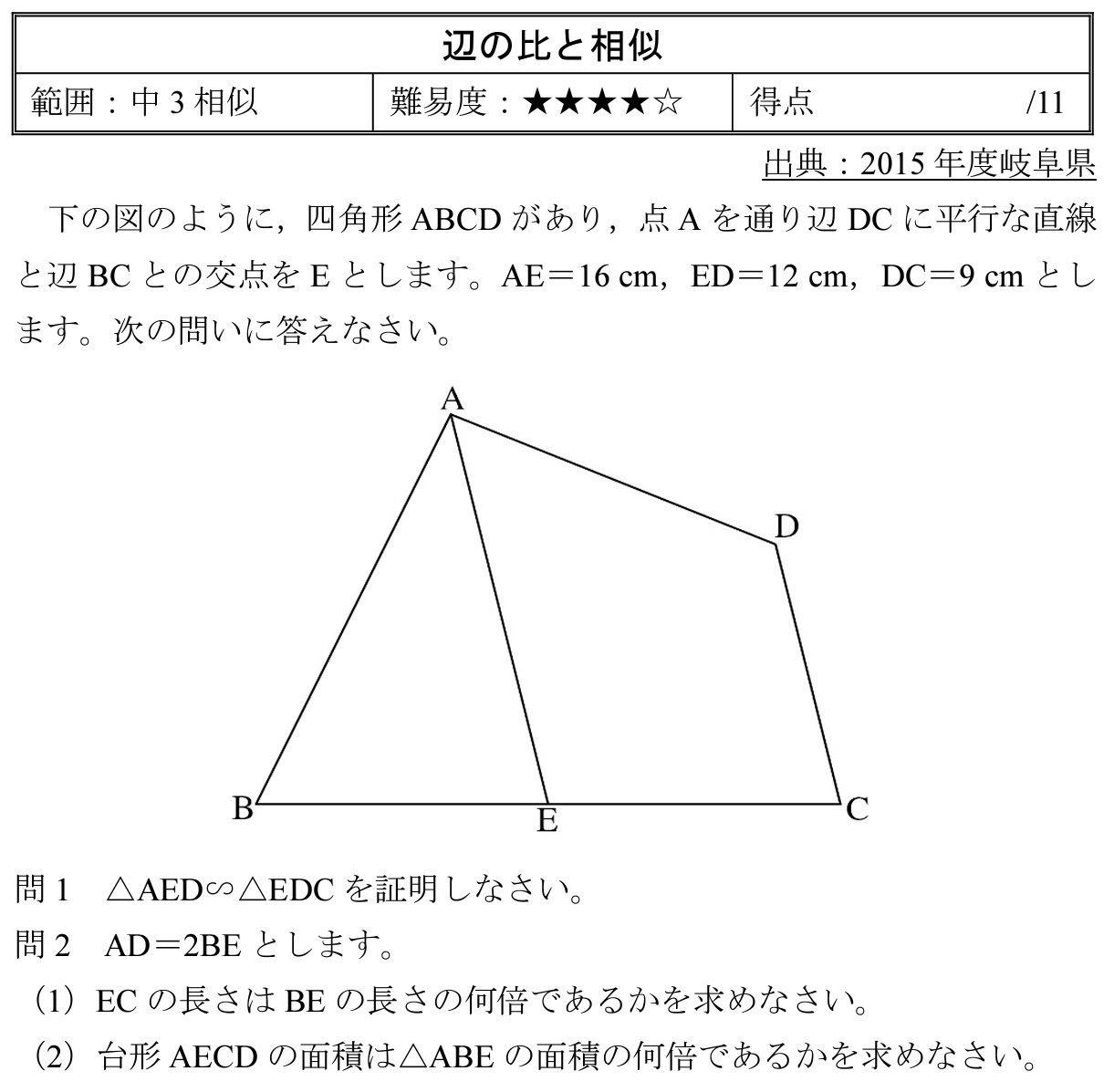



相似比辺の比 15年度岐阜県 高校入試 数学 良問 難問




中3数学 相似 08 平行線と線分の比 解説 練習問題 Youtube
ガリバー旅行記に出てくる数学 相似な図形の面積比や体積比が! 4 4つの問題に挑戦しませんか 高校数学も,図形を使えば中学生にだって 5 数学の勉強法(?) 大層なものではありませんが・・・ 6 一筆(ひとふで)書きの秘密 あなたも一筆書きの天才(? 今回は, 14年度大阪府Bの問題 です。 えげつない問題もあるのですが,中には計算は面倒くさくないけど,ひたすら思いつくのが難しいというちょうどよい問題もあります。 面白い問題が多いので,どこの都道府県でもうまく使えそう。 第19回芸術的な難問高校入試 「惑わす相似」 出典:14年度 大阪府高校入試 過去問 数学B 範囲:相似,三平方の定理など中3数学相似の基本性質をわかりやすく問題解説! 相似な図形 相似平行線と比の利用、辺の長さを求める方法をまとめて問題解説!



相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス




相似な図形 無料で使える中学学習プリント
中学生の数学学習サイト 中学生の数学学習サイトは、中学1年から3年までの家庭で使える練習問題プリントや各単元の要点を紹介しているサイトです。 学年ごとで基礎から発展問題まで幅広く活用できる構成となっています。 中学生の数学学習サイト 数学 > 数学 中学生数学苦手No2!?「相似」ならば(4)(5)(6)は言えるが,(4)(5)(6)から「相似」というためには「間の角が等しい」ことを追加しなければならない. 例題1 異なる4点 A, B, C, D が同一円周上にあって,線分 AB と線分 CD の交点を P とするとき



1




辺の比 面積比 相似 16年東京都 高校入試 数学 良問 難問
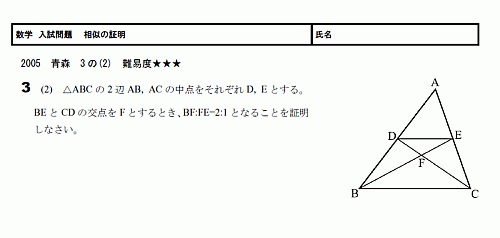
三角形bdcと三角形bfeは相似なので、dc:fe=2:1。 2:1=6:fe。fe=3m。 解答:(1)16m (2)3m 相似の解説ページ 練習問題 算数目次 算数・数学 のページ数学35章図形と相似「平行線と線分の比」<準備問題> 組 番 名前 1平行四辺形の定義を書きなさい。 2四角形が平行四辺形であるための条件が3つ書いてあります。あと2つ,条件を書きなさい。 ・2組の向かい合う辺がそれぞれ平行である。#三角形の相似条件 #相似 #線分比 今回は、相似の2回目。相似な三角形の線分比を学びます。解説のとおりにすれば、どんな問題も簡単に解けます。
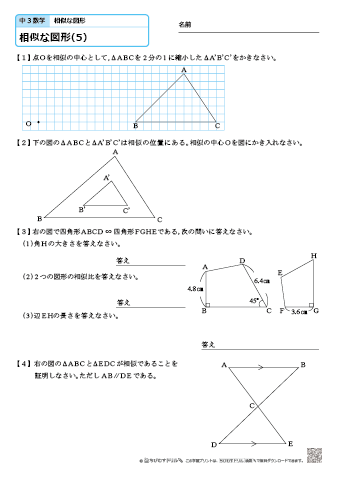



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




三角形の相似条件が見やすい図で一発理解できる 練習問題付き 高校生向け受験応援メディア 受験のミカタ
中学数学の演習問題の解法の解説をしたいと思います。 お役に立てばうれしいです。 合同と相似の証明問題の流れ 合同や相似を証明する問題の解き方についてです。 解答すべき内容が示されているので比較的得点しやすい問題になります。 練習を中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード・印刷 相似な図形のかき方、三角形の相似条件や、相似を利用した距離や高さの求め方を練習していきます。相似と面積比,体積比を絡ませた良い練習問題。 ・ポンデリング空間図形(★★★★☆)(17年度熊本県) 図が可愛らしい問題。 ・超楽しい空間図形(一部中1でも解ける)(★★★★☆)(年度立川高校) とてもとてもきれいな問題。




世界一わかりやすい数学問題集中3 5章 図形と相似
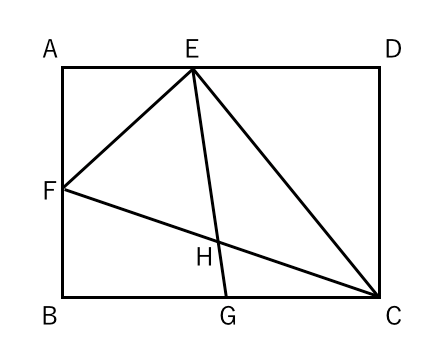



相似の問題10 テスト 受験対策 苦手な数学を簡単に
公立高校入試 過去問 英語 お問い合わせ 全都道府県 公立高校入試 過去問 数学 4平面図形 4相似の証明ほか 10/18 公立高校入試 過去問 数学 目次 数学4.平面図形 4.相似の証明 複合問題ほか 数学4.平面図形 4.相似の証明 複合問題ほか 02年度常に相似である図形 問題(2 学期期末) 次の各組の図形は常に相似であるといえるか。いえる場合は ,いえない場合は×で答え よ。 (1) 2 つの二等辺三角形 (2) 2 つの正三角形 (3) 2 つの直角三角形 (4) 2 つのひし形 (5) 2 つの正五角形 解答欄 (1)中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード・印刷 お気に入り 教材の新学習指導要領への対応について



Homeroom 数学の入試問題を解くとき大切なこと 正しい入り口から入らないと問題は解けない 平面図形 相似 働きアリ The 2nd



相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス
三角形の相似条件 相似の問題の中でも、三角形の相似を証明する問題が多く出題されます。 ここでは、三角形の相似を証明するために必要な3つの条件を説明します。 私が実際に問題を解いた時に使う回数が多いと感じた順に書いてみました。 1つめは、 「2組の辺の比とその間の角が等しい」 という条件です。 個人的には一番使う回数が多いと感じました図形と相似の問題 Try IT(トライイット)の図形と相似の様々な問題を解説した映像授業一覧ページです。 図形と相似を探している人や問題の解き方がわからない人は、単元を選んで問題と解説の映像授業をご覧ください。




相似な図形の面積比の問題 相似比を出してから二乗しよう 中学や高校の数学の計算問題



中学数学単元別 相似な図形 数学 中学校 教材 問題集 305 学林舎 通販 Yahoo ショッピング



高校入試数学 相似な三角形の対策問題



中3数学12 図形の相似2 相似条件と証明 基本解説プリント 問題 327
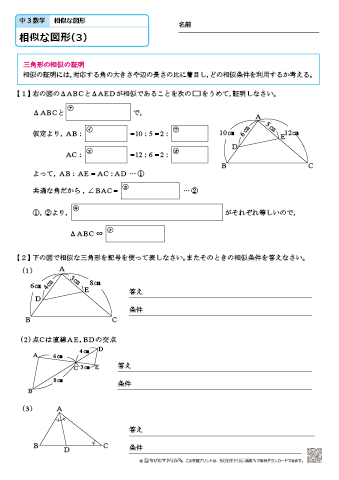



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




世界一わかりやすい数学問題集中3 5章 図形と相似



中3数学 標準問題 問題 329 図形の相似4 中点連結定理 プリント




三角形の相似条件が見やすい図で一発理解できる 練習問題付き 高校生向け受験応援メディア 受験のミカタ




無料 中3数学 標準問題 解答プリント 328 図形の相似3 線分の比
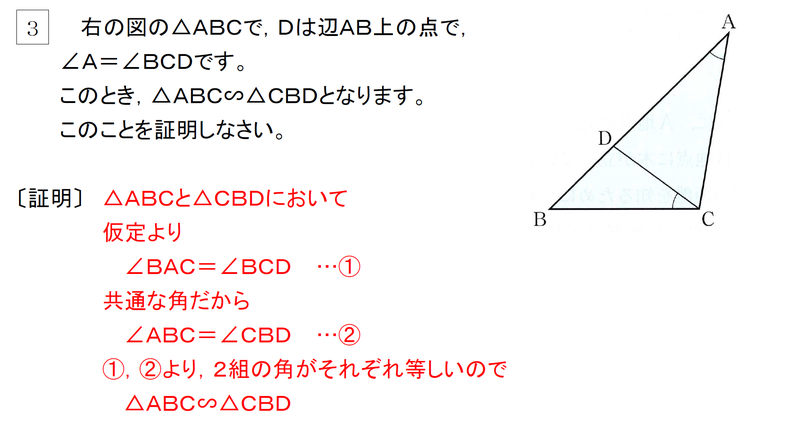



中学3年 数学 東京書籍 新しい数学 相似な図形 平行線と比 赤城 ᐡᐤᐡ
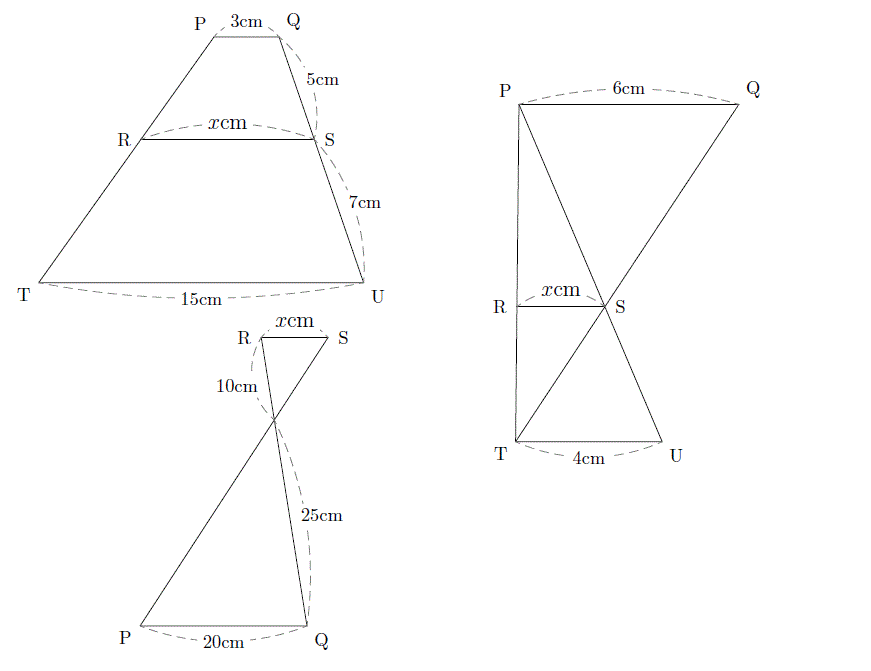



かみのドリル 相似



相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス
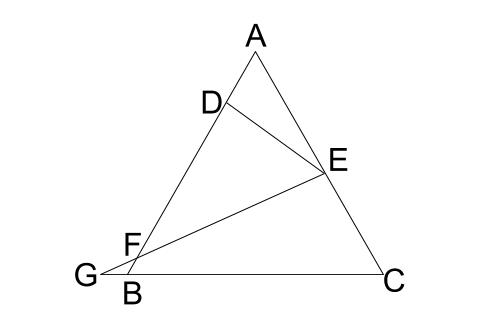



難問 正三角形の相似 中学数学の無料オンライン学習サイトchu Su




世界一わかりやすい数学問題集中3 5章 図形と相似




三角形の相似条件と証明問題の解き方 数学fun




都立入試 数学 図形の証明問題 大問4問2 図形の相似のひみつ 都立高校入試で成功する方法
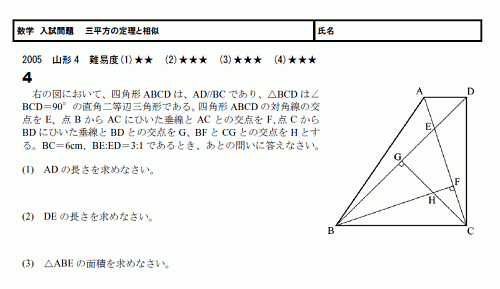



数学 高校入試 無料学習プリント教材




最高中3 数学 相似 子供向けぬりえ




数学 中3 53 相似と面積 応用編 Youtube
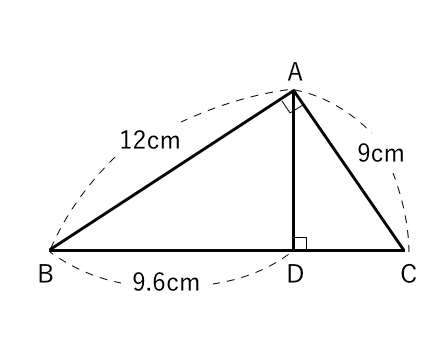



相似の問題 テスト 受験対策 苦手な数学を簡単に
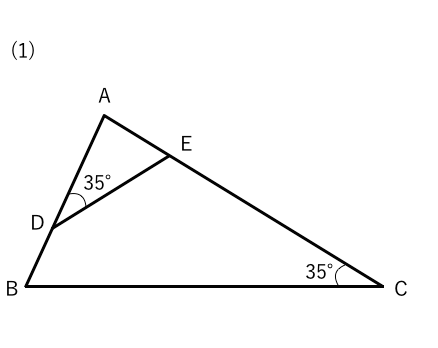



相似な図形 相似条件の練習問題 苦手な数学を簡単に




高校入試対策数学 面積比に関する対策問題 Pikuu
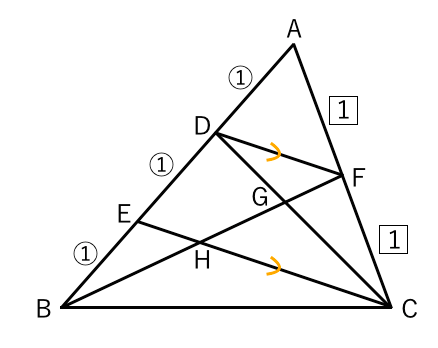



相似な図形 平行線と線分の比 よく出る系 苦手な数学を簡単に




意外と解けない相似問題 中3教科書レベルの基本問題 暇つぶしに動画で脳トレ




三角形の相似条件が見やすい図で一発理解できる 練習問題付き 高校生向け受験応援メディア 受験のミカタ




世界一わかりやすい数学問題集中3 5章 図形と相似
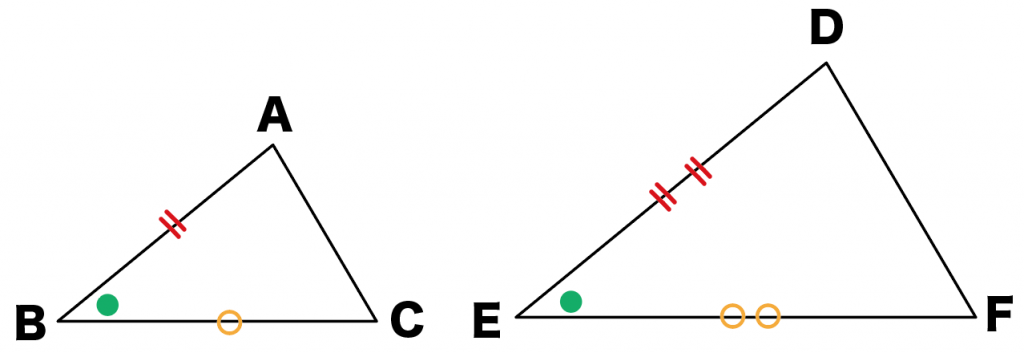



中学数学 相似の証明問題の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
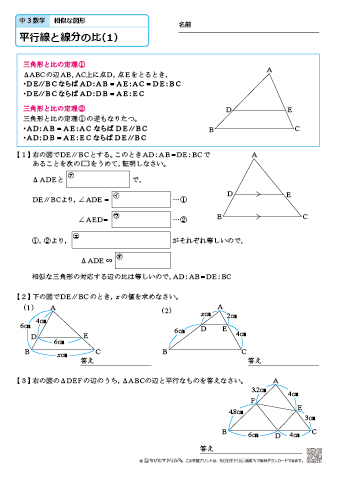



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
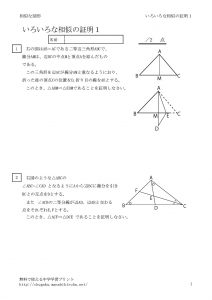



いろいろな相似の証明 無料で使える中学学習プリント




4の問題です 相似を用いて求めたのですが もっと単純な求め方はありますか 数学得 Clear
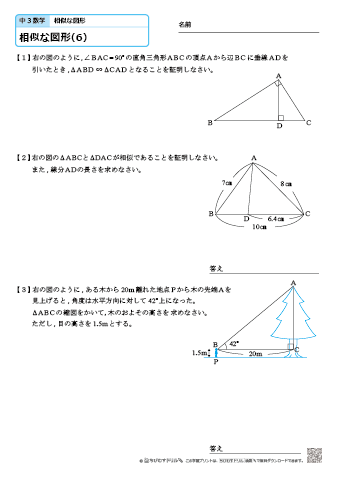



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中3数学 相似比とは 例題編 映像授業のtry It トライイット



中3数学12 図形の相似4 中点連結定理 縮図 基本問題プリント 問題 329



中3数学 相似の 差がつく 問題 成績 上がってます 根城学習塾 八戸市




中3数学基礎 本当に使える裏技 相似の問題で差をつけろ 定期テストや高校入試に レオンの中学数学探検所




相似比の利用 スタディーx




相似の面積比を求める問題 上級編 Youtube
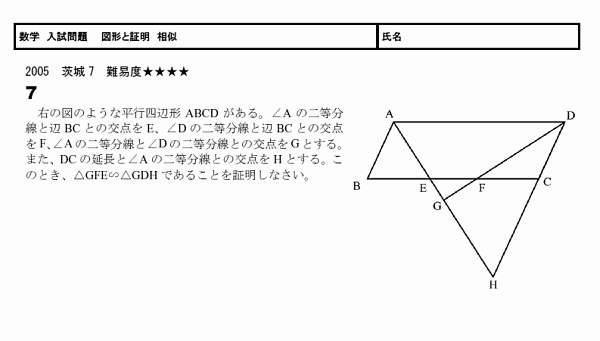



図形と証明 相似 無料学習プリント教材



Studydoctor相似比と面積の計算 中学3年数学 Studydoctor



中3数学 相似や比の応用問題を解くためのテクニック 個別指導塾のyou 学舎日記 公式ブログ
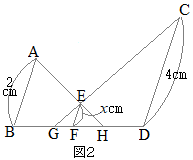



相似図形 高校入試問題




数学 中3 48 相似の証明チャレンジ Lv 3 Youtube
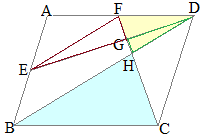



相似図形 高校入試問題
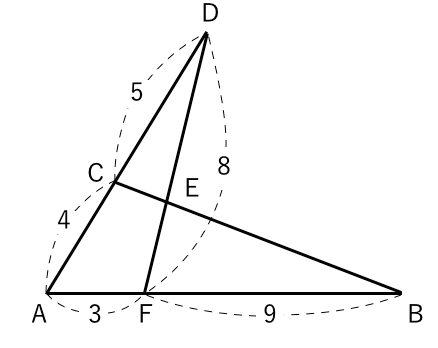



相似の問題19 テスト 受験対策 苦手な数学を簡単に




三平方の定理と相似の問題 無料で使える中学学習プリント




世界一わかりやすい数学問題集中3 5章 図形と相似



中3数学 相似な図形の線分比の定期テスト対策問題 Examee
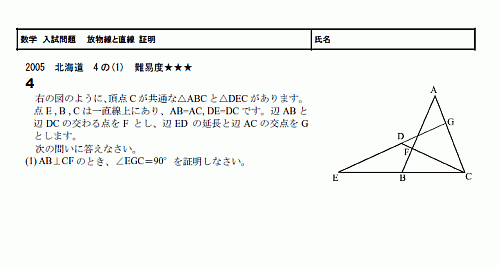



図形と証明 相似 スタディーx




中学3年 数学 東京書籍 新しい数学 相似な図形 平行線と比 赤城 ᐡᐤᐡ




数学a 図形の性質 以下の問題の解説赤線部について 相似条件は 3辺が等しい Clear




中学3年の数学 動画 相似と面積 基本編の問題 19ch




裏返しの相似 数学のすすめ




中3数学 相似の証明問題 練習編 映像授業のtry It トライイット




世界一わかりやすい数学問題集中3 5章 図形と相似
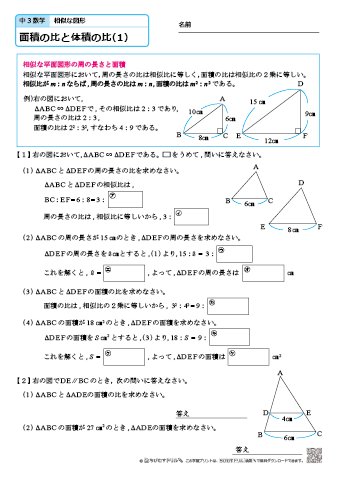



中学3年生 数学 面積の比と体積の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
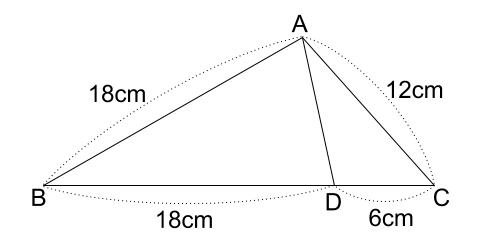



中学数学 相似の証明 その1 中学数学の無料オンライン学習サイトchu Su




中学数学の図形相似問題を解説してください Okwave
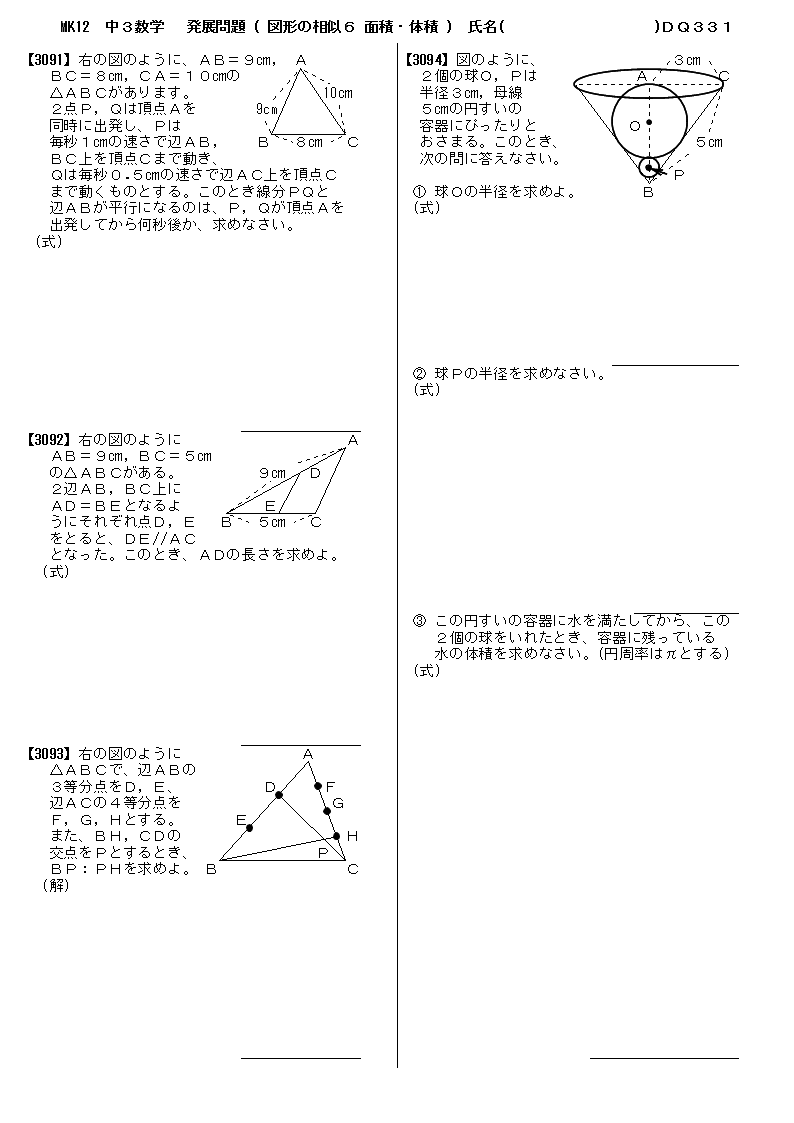



無料 中3数学 発展 応用問題 問題プリント 331 図形の相似6 面積比 体積比
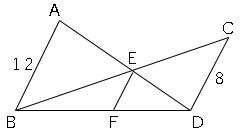



図形と相似の練習問題 数学の要点まとめ 練習問題一覧




Math 相似 相似の難問を ちょうちょ と おむすび で簡単に解く 2 働きアリ
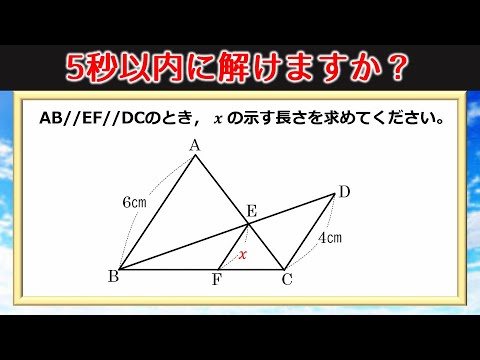



図形問題 知っている人は5秒で解ける相似の裏技 Youtube
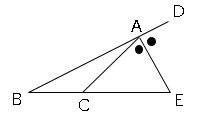



図形と相似の練習問題 数学の要点まとめ 練習問題一覧



相似の問題 テスト 受験対策 苦手な数学を簡単に



図形と証明 相似 スタディーx




中学3年 数学 東京書籍 新しい数学 相似な図形 平行線と比 赤城 ᐡᐤᐡ




中3数学 相似 台形の対角線 Youtube



中3数学 相似や比の応用問題を解くためのテクニック 個別指導塾のyou 学舎日記 公式ブログ




これで点が取れる 単元末テスト 中3数学 5章 図形と相似



相似の問題 テスト 受験対策 苦手な数学を簡単に



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中学3年 数学 東京書籍 新しい数学 相似な図形 平行線と比 赤城 ᐡᐤᐡ
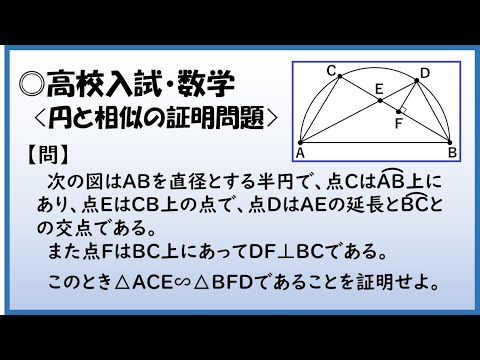



高校入試 数学 円と相似の証明問題 Youtube




相似 無料で使える中学学習プリント



相似の問題23 テスト 受験対策 苦手な数学を簡単に




無料 中3数学 基本問題 解答プリント 図形の相似2 相似条件と証明




相似な図形 中3数学期末テスト対策問題 赤城 ᐡᐤᐡ



3
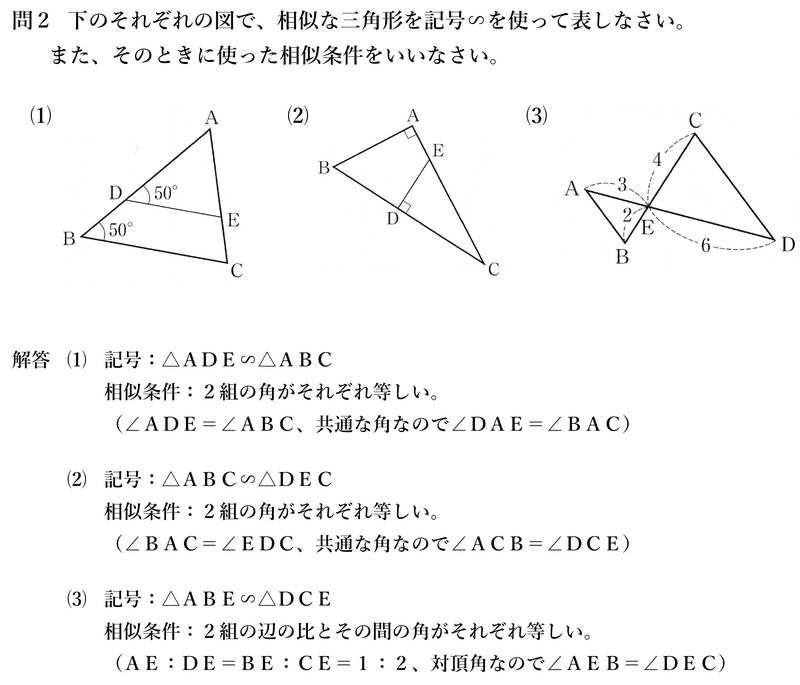



中学3年 数学 東京書籍 相似条件 練習問題 赤城 ᐡᐤᐡ



1
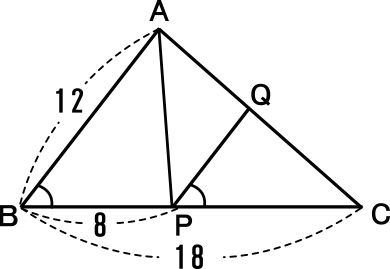



中学3年数学練習問題 図形と相似の定期テスト対策問題




数学 相似の問題 三角形の面積 相似の問題なのですが わからない問題が Okwave




相似な図形 補助線を引いて考える相似の問題 中学生からの質問 数学 進研ゼミ中学講座 中ゼミ
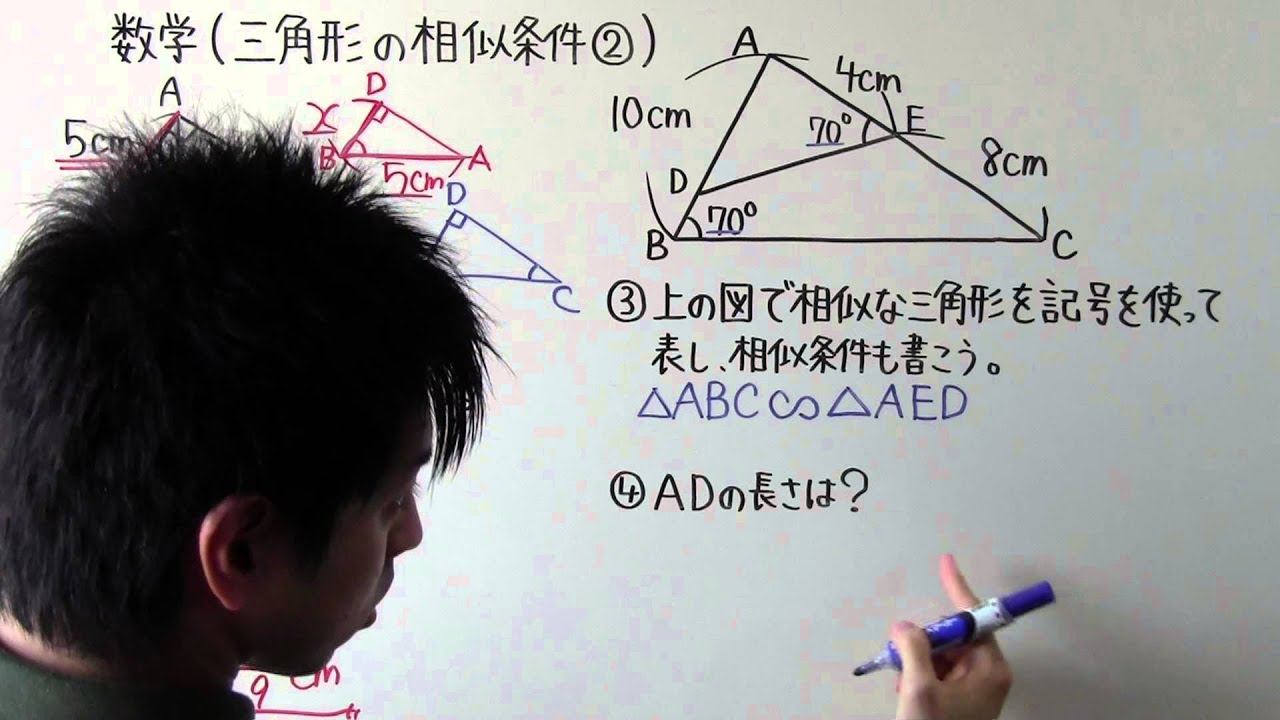



数学 中3 45 三角形の相似条件 Youtube
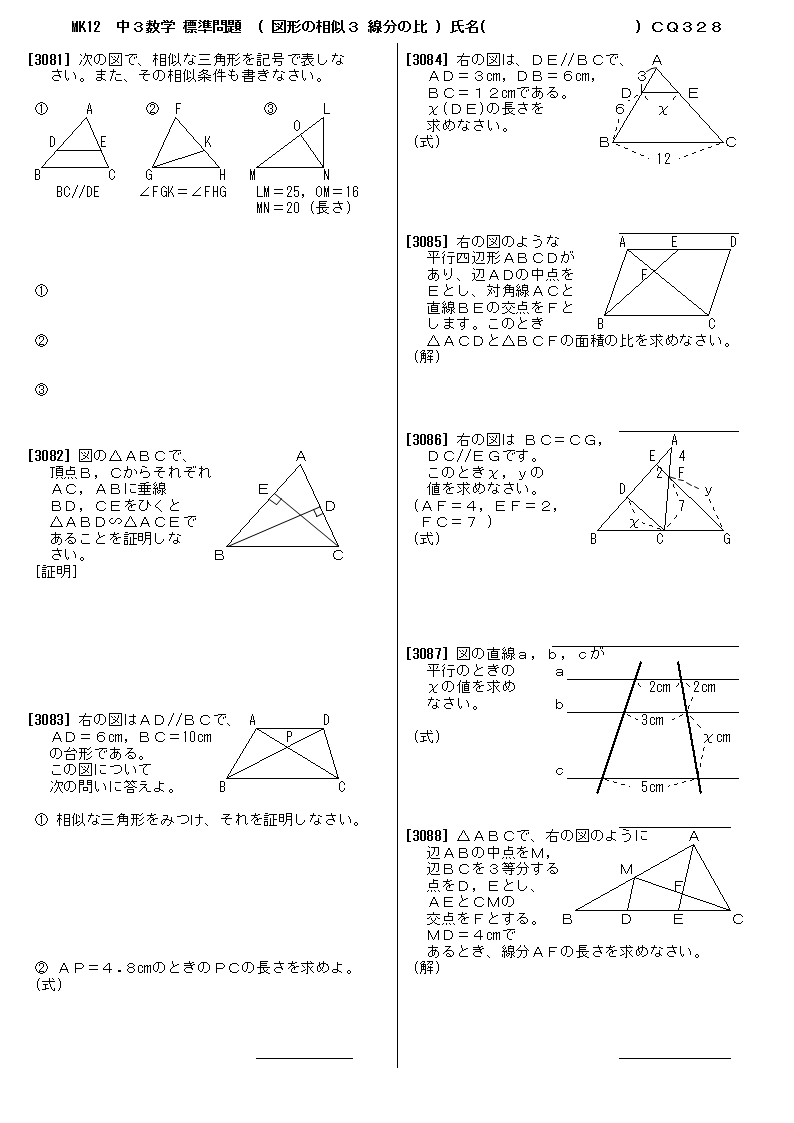



無料 中3数学 標準問題 問題プリント 328 図形の相似3 線分の比
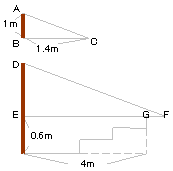



相似 練習問題 解答と解説
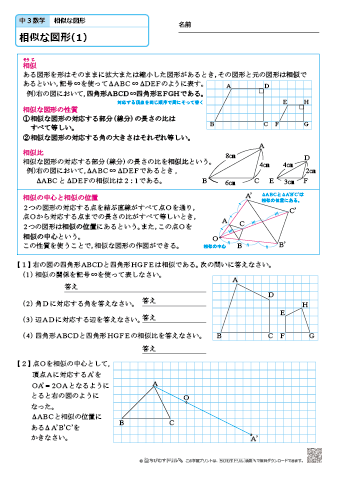



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



相似xを求める問題で 解説を見ても分かりませんでした 教えて下 Yahoo 知恵袋



中3数学12 図形の相似3 線分の比 発展問題プリント 問題 328



0 件のコメント:
コメントを投稿